Prediction of Diabetes Diagnosis via Machine Learning
- Leandro Oliveira

- Nov 5, 2020
- 15 min read
Updated: Nov 6, 2020

Introduction
Data science has been constantly used in diagnostics in the health area. This article presents some machine learning techniques used to make predictions of diagnoses of diabetic patients using the Python language.
Objective
Create a predictive model that is able to predict whether or not a person can develop diabetes. For this, we will use historical patient data, available in the dataset below.
Dataset: Pima Indians Diabetes Dataset http://archive.ics.uci.edu/ml/datasets/diabetes
This dataset describes the medical records among Pima Indians patients and each record is marked whether or not the patient developed diabetes.
Initially, it is important to present a dataset approach below.
Attribute information:
Number of times pregnant
Plasma glucose concentration a 2 hours in an oral glucose tolerance test
Diastolic blood pressure (mm Hg)
Triceps skin fold thickness (mm)
2-Hour serum insulin (mu U/ml)
Body mass index (weight in kg/(height in m)^2)
Diabetes pedigree function
Age (years)
Class variable (0 or 1)
Python Libraries
Firstly, we have to import some libraries to work with data manipulation, data visualization and machine learning.
As we develop our model, we will present more details on the features and applicability of the different algorithms that we will be using.
Although there are popular algorithms that generally have better adherence to some cases, good practice recommends performing tests with different algorithms and choosing the ones that in fact have the best accuracy.
Another important factor to find the best accuracy, will be to find the best hyperparameters of the algorithms and for that we will present some examples of how to do this using Python, because when we use the cloud environment this can be done automatically.
Especially in the health area, where we deal with people's lives and we need to obtain the best possible accuracy and avoid Error I and Error II.
We will present each algorithm within a template, thus allowing the use of it outside that project.
The process becomes more and more efficient when we work with templates that require the lowest possible level of customization, as this facilitates the development process.
Many cloud providers have been applying this technique in their development environments. Microsoft Azure for example acts strongly in the process of automating and standardizing templates that require little customization.
The cloud environment makes it easy to carry out the testing of various algorithms and hyperparameters in a practical and efficient way, thus reducing production time and minimizing errors.
As in this project we will not use the cloud environment, we will demonstrate the main steps of the machine learning technique that can be applied to the classification method via Python.
We will also present the versions of the libraries and the Python version to prevent errors for configuration of the environment.

Fig. 1. Libraries Versions and Python Version
Extracting and Loading Data
There are several considerations when uploading data to the Machine Learning process. For example: does your data have a header? If not, you will need to define the title for each column. Do your files have comments? What is the column delimiter? Are some data in quotes, single or double?

Fig.2 Loading the data
Exploratory Data Analysis
Descriptive statistics
After importing the data, we need to apply descriptive statistics techniques to present the data. This process introduces a better understanding of the data and in many cases we were able to identify patterns and outliers in the distribution of the data.

Fig.3 Top 20 lines
If the number of lines in your file is very large, the algorithm can take a long time to be trained. If the number of records is too small, you may not have enough records to train your model.
If you have many columns in your file, the algorithm may have performance problems due to the high dimensionality.
The best solution will depend on each case. But remember: train your model in a subset of your larger data set and then apply the model to new data.
The type of data is very important. It may be necessary to convert strings, or columns with integers can represent categorical variables or ordinary values.
Below we will present a general approach on the data

Fig. 4 Statistics summary and Data type.
Balancing the classes
In classification problems it may be necessary to balance the classes. Unbalanced classes (ie, greater volume of one of the class types) are common and need to be addressed during the pre-processing phase. We can see below that there is a clear disproportion between classes 0 (non-occurrence of diabetes) and 1 (occurrence of diabetes).

Fig.5 Unbalanced Distribution.
Synthetic Minority Oversampling Technique (SMOTE)
A problem with unbalanced classification is that there are few examples from the minority class for a model to effectively learn the decision boundary.
One way to solve this problem is to over-show the examples in the minority class. This can be achieved by simply duplicating minority class examples in the training data set before adjusting a model. This can balance the distribution of classes, but it does not provide any additional information to the model.
An improvement in duplicating examples from the minority class is to synthesize new examples from the minority class. This is a type of data augmentation for tabular data and can be very effective.
Below we present the steps for this process.

Fig.5 Balanced class distribution.
Correlation analysis
The correlation is the relationship between 2 variables. The most common method for calculating correlation is the Pearson method, which assumes a normal distribution of data. Correlation of -1 shows a negative correlation, while a correlation of +1 shows a positive correlation. A correlation of 0 shows that there is no relationship between the variables.
Some algorithms such as linear regression and logistic regression can present performance problems if there are highly correlated (collinear) attributes.
Below we present the steps for this process.

Fig. 6 Correlation Analysis.
Skewness Analyse
Skewness refers to distortion or asymmetry in a symmetrical bell curve, or normal distribution, in a set of data. If the curve is shifted to the left or to the right, it is said to be skewed. Skewness can be quantified as a representation of the extent to which a given distribution varies from a normal distribution. A normal distribution has a skew of zero, while a lognormal distribution, for example, would exhibit some degree of right-skew.
Negatively-skewed distributions are also known as left-skewed distributions. Skewness is used along with kurtosis to better judge the likelihood of events falling in the tails of a probability distribution.

Fig.7 Skew Analyse
Visualization with Matplotlib
Matplotlib is a Python library for building data visualization. With the histogram we can quickly assess the distribution of each attribute. Histograms group data into bins and provide a count of the number of observations in each bin. With the histogram, you can quickly check the symmetry of the data and whether it is in normal distribution or not. This will also help in identifying outliers.
We can see that the attributes that have an exponential distribution such as Test attribute. In another hand, we can see that the mass and press columns have a normal distribution.

Fig.8 Data visualization with Matplotib.

Fig. 9 Seaborn Visualization

Fig.10 Seaborn data visualization
Preparing the Data for Machine Learning
Many algorithms expect to receive data in a specific format. It is your job to prepare the data in a structure that is suitable for the algorithm you are using.
It is very likely that you will have to perform pre-processing tasks on the data. This is a necessary step within the process. The challenge is the fact that each algorithm requires a different structure, which may require different transformations in the data. But it is possible in some cases to obtain good results without pre-processing work. But it is good practice to create different views and transformations of the data, in order to be able to test different Machine Learning algorithms.
Normalization - Méthod 1
The first tasks within pre-processing, is to put your data on the same scale. Many Machine Learning algorithms will benefit from this and produce better results. This step is also called normalization and means putting the data on a scale with a range between 0 and 1. This is useful for optimization, being used in the core of Machine Learning algorithms, such as gradient descent. This is also useful for algorithms such as regression and neural networks and algorithms that use distance measurements, such as KNN. Scikit-learn has a function for this step, called MinMaxScaler (). It is important to remember that data normalization is not applied to qualitative data.

Fig. 11 Normalization Method 1 - MinMaxScaler
Normalization - Méthod 2
In scikit-learn, normalization refers to adjusting the scale of each observation (line) so that it has a length of 1 (called a vector of length 1 in linear algebra). This pre-processing method is useful when we have sparse datasets (with many zeros) and attributes with a wide range of scales. Useful when using neural network algorithms or using distance measurement, such as KNN. Scikit-learn has a function for this step, called Normalizer ().

Fig.12 Normalization Method 2 - Normalizer
Standardization
Standardization is the technique for transforming attributes with Gaussian distribution (normal) and different means and standard deviations into a Gaussian distribution with mean equal to 0 and standard deviation equal to 1. This is useful for algorithms that expect data to have a Gaussian distribution, such as linear regression, logistic regression and linear discriminant analysis. It works well when the data is already on the same scale. Scikit-learn has a function for this step, called StandardScaler ().

Fig.13 Standardization.
Binarization (Transform the Data in Binary Values)
We can define a value in our data, which we call a threshold and then we define that all values above the threshold will be marked as 1 and all values equal to or below the threshold will be marked as 0. This is what we call Binarization . This is useful when we have probabilities and want to make the data more meaningful. Scikit-learn has a function for this step, called Binarizer ().

Fig.14 Binarization
Feature Selection
The attributes present in your dataset and which you use in the training data, will have a great influence on the accuracy and result of your predictive model. Irrelevant attributes will have a negative impact on performance, while collinear attributes can affect the accuracy of the model. Scikit-learn has functions that automate the work of extracting and selecting variables.
The Feature Selection step is where we select the attributes (variables) that will be the best candidates for predictor variables. Feature Selection helps us to reduce overfitting (when the algorithm learns too much), increases the accuracy of the model and reduces training time.
Univariate Selection
Statistical tests can be used to select the attributes that have a strong relationship with the variable we are trying to predict. Scikit-learn provides the SelectKBest () function that can be used with various statistical tests to select attributes. We will use the chi-square test and select the 4 best attributes that can be used as predictor variables.

Fig.15 Univariate Statistical Test
Recursive Attribute Elimination
This is another technique for selecting attributes, which recursively removes the attributes and builds the model with the remaining attributes. This technique uses the accuracy of the model to identify the attributes that most contribute to predict the target variable. In English this technique is called Recursive Feature Elimination (RFE).
The example below uses the technique of recursive attribute elimination with a Logistic Regression algorithm to select the 3 best predictor variables. The RFE selected the preg, mass and pedi variables, which are marked as True in "Selected Attributes" and with a value of 1 in "Attribute Ranking".

Fig.16 Recursive Elimination of Variables
Ensemble Method for Selection of Variables
Bagged Decision Trees, like the RandomForest algorithm (these are called Ensemble Methods), can be used to estimate the importance of each attribute. This method returns a score for each attribute.
The higher score meaning the greater importance of the attribute.

Fig.17 Extra Tree Classifier
Dimension Reduction (Feature Extraction)
Principal Component Analysis (PCA)
PCA was invented in 1901 by Karl Pearson and uses linear algebra to transform datasets into a compressed form, which is generally known as Dimensionality Reduction. With PCA you can choose the number of dimensions (called main components) in the transformed result. We will use PCA to select 3 main components.
Principal Component Analysis (PCA) is a method for extracting important variables (in the form of components) from a large set of variables, available in a data set. This technique allows you to extract a small number of dimensional sets from a highly dimensional dataset. With fewer variables the visualization also becomes much more significant. PCA is most useful when dealing with 3 or more dimensions.
Each resulting component is a linear combination of n attributes. That is, each main component is a combination of attributes present in the dataset. The First Principal Component is the linear combination of attributes with maximum variance and determines the direction in which there is the highest variability in the data. The greater the variability captured in the first main component, the more information will be captured by the component. The Second Main Component captures the remaining variability. All subsequent components have the same concept.
The PCA needs to be fed normalized data. Using the PCA on non-normalized data can generate unexpected results.
Principal component analysis is a multivariate statistical technique that consists of transforming a set of original variables into another set of variables called principal components. The main components have important properties: each main component is a linear combination of all the original variables, they are independent of each other and are estimated with the purpose of retaining, in order of estimation, the maximum information, in terms of the total variation contained in the data . The main components are guaranteed to be independent only if the data is normally distributed (jointly).
The aim is to redistribute the variation observed in the original axes in order to obtain a set of unrelated orthogonal axes. This technique can be used to generate indexes and group individuals. The analysis groups individuals according to their variation, that is, individuals are grouped according to their variances, that is, according to their behavior within the population, represented by the variation in the set of characteristics that define the individual, that is, the technique groups individuals of a population according to the variation of their characteristics.
Principal component analysis is associated with the idea of reducing data mass, with the least possible loss of information.
The goal is to summarize the data that contains many variables (p) by a smaller set of composite variables (k) derived from the original set. PCA uses a data set represented by an array of n records by p attributes, which can be correlated, and summarizes this set by uncorrelated axes (main components) that are a linear combination of the original p variables. The first k components contain the largest amount of variation in the data.
In general terms, the PCA seeks to reduce the number of dimensions of a dataset, projecting the data on a new plane. Using this new projection, the original data, which can involve several variables, can be interpreted using fewer "dimensions." In the reduced dataset we can see trends, patterns and / or outliers more clearly. But it is worth remembering that the rule: "If it is not in the raw data it does not exist!" is always valid. The PCA provides only more clarity to the standards that are already there.
The greater variance meaning the greater amount of information contained in the component.

Fig.18 Feature Extraction
Resampling
You need to know if your predictive model will work well when you receive new data. The best way to evaluate model performance is to make predictions on data that you already know the result. Another way to test your model's performance is to use statistical techniques such as sampling methods that allow you to estimate how well your model will make predictions on new data.
The model evaluation is an estimate of how well the algorithm will be able to predict in new data. This does not guarantee performance. After evaluating the model, we can re-train it with training data and then prepare it for operational use in production. There are several techniques for this and we will study two here: Training and test dataset and Cross Validation.
Training and Test Data
This is the most used method to evaluate the performance of a Machine Learning algorithm. We split our original data into training and test data. We train the algorithm on the training data and make predictions on the test data and evaluate the result. The division of the data will depend on your dataset, but sizes between 70/30 (training / test) and 65/35 (training / test) are often used.
This method is very fast and ideal for very large data sets. The negative point is the possibility of high variance.

Fig. 19 Training and Test data with Logistic Regression
Cross Validation
Cross Validation is a technique that can be used to evaluate the performance of a model with less variance than the technique of dividing data in training / testing. With this technique we divide the data into parts usually called k-folds (for example k = 5, k = 10). Each part is called fold. The algorithm is trained in k-1 folds. Each fold is used in training repeatedly and one fold at a time. After executing the process in k-1 folds, we can summarize the performance in each fold using the average and the standard deviation (I said that Statistics was important in the Big Data Analytics process). The result is usually more reliable and offers greater accuracy to the model. The key to this process is to define the correct k value, so that the number of folds adequately represents the number of repetitions required.

Fig. 20 Cross Validation
Evaluating Performance
The metrics you choose to evaluate model performance will influence how performance is measured and compared to models created with other algorithms.
We will use the same algorithm, but with different metrics and thus compare the results. The cross_validation.cross_val_score () function will be used to evaluate performance.
Metrics for Classification Algorithms

Fig.21 Two different results for Logistic Regression with different parameters.

Fig.22 Confusion Matrix
Classification Report
A Classification report is used to measure the quality of predictions from a classification algorithm. How many predictions are True and how many are False. More specifically, True Positives, False Positives, True negatives and False Negatives are used to predict the metrics of a classification report as shown below.
Precision – What percent of your predictions were correct?
Precision is the ability of a classifier not to label an instance positive that is actually negative. For each class it is defined as the ratio of true positives to the sum of true and false positives.
TP – True Positives FP – False Positives Precision – Accuracy of positive predictions. Precision = TP/(TP + FP)
Recall – What percent of the positive cases did you catch?
Recall is the ability of a classifier to find all positive instances. For each class it is defined as the ratio of true positives to the sum of true positives and false negatives.
FN – False Negatives
Recall: Fraction of positives that were correctly identified. Recall = TP/(TP+FN)
F1 score – What percent of positive predictions were correct?
The F1 score is a weighted harmonic mean of precision and recall such that the best score is 1.0 and the worst is 0.0. Generally speaking, F1 scores are lower than accuracy measures as they embed precision and recall into their computation. As a rule of thumb, the weighted average of F1 should be used to compare classifier models, not global accuracy.
F1 Score = 2*(Recall * Precision) / (Recall + Precision)

Fig.23 Classification Report.
Classification Algorithms
We have no way of knowing which algorithm will work best in building the model, before we test the algorithm with our dataset. The ideal is to test some algorithms and then choose the one that provides the best level of accuracy. We will test a set of classification algorithms, under the same conditions.
The next code below will present a template where we can test the algorithms at the same time to evaluate and compare the results.

Fig.24 Predictive Model Selection
Predictive Model Selection
We will see that the Logistic Regression and Linear Discriminant Analysis algorithms showed the best level of precision.
Model Optimization - Adjusting Hyperparameters
All Machine Learning algorithms are parameterized, which means that you can adjust the performance of your predictive model, through the tuning (fine tuning) of the parameters. Your job is to find the best combination between the parameters in each Machine Learning algorithm. This process is also called Hyper Parameter Optimization. Scikit-learn offers two methods for automatic parameter optimization: Grid Search Parameter Tuning and Random Search Parameter Tuning.
Grid Search Parameter Tuning
This method methodically performs combinations between all parameters of the algorithm, creating a grid. We will try this method using the Logistic Regression algorithm.

Fig.25 Logistic Regression with Grid Search Parameter Tuning.
Random Search Parameter Tuning
This method generates samples of the parameters of the algorithms from a uniform random distribution for a fixed number of iterations. A model is built and tested for each combination of parameters.
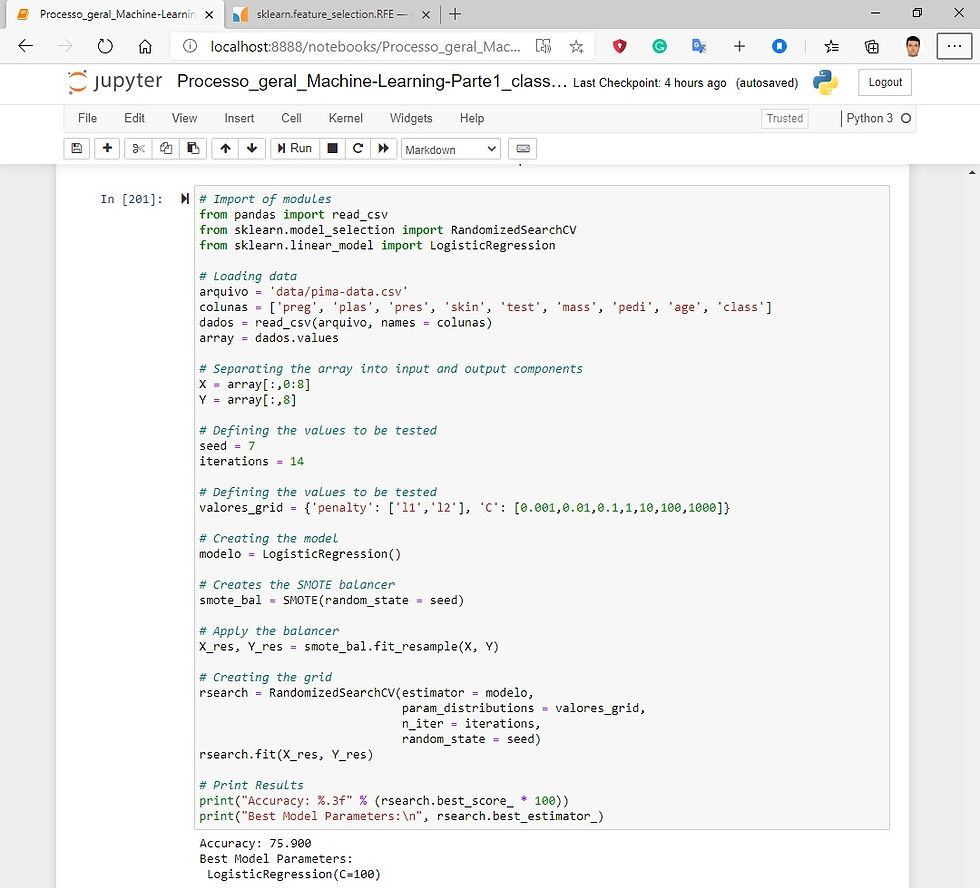
Fig.26 Logistic Regression with Random Search Parameter Tuning.
Optimizing Performance with Ensemble Methods
Ensemble methods allow you to considerably increase the level of accuracy in your predictions. We'll look at how to create some of the most powerful Ensemble Methods in Python. There are 3 main methods for combining predictions from different models:
Bagging - For building multiple models (usually of the same type) from different subsets in the training dataset.
Boosting - Para construção de múltiplos modelos (normalmente do mesmo tipo), onde cada modelo aprende a corrigir os erros gerados pelo modelo anterior, dentro da sequência de modelos criados.
Voting - For building multiple models (usually of different types) and simple statistics (like the average) are used to combine the predictions.
Let's see how to use these methods.
Bagged Decision Trees
This method works well when there is high variance in the data.

Fig.27 Bagged Decision Trees
Random Forest
Random Forest is an extension of the Baggig Decision Tree. Samples of the training dataset are used with replacement, but the trees are created in a way that reduces the correlation between individual classifiers (Random Forest is a set of decision trees).

Fig.28 Random Forest
AdaBoost
Algorithms based on Boosting Ensemble create a sequence of models that try to correct the errors of the previous models within the sequence. Once created, models make predictions that can be weighted according to their accuracy and the results are combined to create a single final forecast.
AdaBoost assigns weights to the instances in the dataset, defining how easy or difficult they are for the classification process, allowing the algorithm to pay more or less attention to the instances during the model construction process.

Fig. 29 AddBoot
Gradient Boosting
Also called Stochastic Gradient Boosting, it is one of the most sophisticated Ensemble methods.

Fig.30 Gradient Boosting.
Voting Ensemble
This is one of the simplest Ensemble methods. This method creates two or more separate models from the training dataset. The Voting Classifier then uses the average of the predictions for each sub-model to make the predictions on new data sets. The predictions of each sub-model can be weighted, either through manually defined parameters or through heuristics. There are more advanced versions of Voting, in which the model can learn the best weight to be assigned to the sub-models. This is called Stacked Aggregation, but it is not yet available in Scikit-learn.

Fig.31 Voting Ensemble.
Algorithm XGBoost - Extreme Gradient Boosting
The XGBoost algorithm is an extension of GBM (Gradient Boosting Method) that allows multithreading on a single machine and parallel processing on a cluster of multiple servers. The main advantage of XGBoost over GBM is its ability to manage sparse data. XGBoost automatically accepts sparse data as input without storing zeros in memory.
Main advantages of XGBoost:
1- Accepts sparse data (which allows working with sparse matrices), without the need for conversion to dense matrices.
2- Build a learning tree using a modern split method (called a quatile sketch), which results in much less processing time than traditional methods.
3- Allows parallel computing on a single machine (through the use of multithreading) and parallel processing on machines distributed in clusters.
Basically XGBoost uses the same parameters as GBM and allows advanced treatment of missing data.
XGBoost is widely used by Data Scientists who win competitions in Kaggle. Github repository: https://github.com/dmlc/XGBoost

Fig.32 Install XGBoost from PyPi
Conclusion
We conclude in this article about the importance of data analysis during the pro-process and about the techniques of Feature engineering and its importance in the final results of the algorithm.
We present the main algorithms, performing tests with different parameters in order to have more options for comparing results.
We verified in Fig.21 that the Logistic Regression with different parameters obtained the best result of the entire development process, with an accuracy of 83,221

Comments